算法&数据结构的学习 #
——算法与复杂度 - 对《挑战程序竞赛》第二辑的摘录(zhaochao) #
引子 #
线索:
算法的使用原则
伪代码书写原则
时间复杂度 大O表示法
对一群选手的成绩进行读取,降序输出前三名的得分,
那么我们容易想到这样三种方法:
1.3次搜索 先找到最大值->剔除->再找到最大值……
2.排序 通过排序算法对存入的数据降序排列,输出前三名。
3.设定容量为100的数组C[n],每个数组单元n记录同分个数。从C[100]开始,做n–,累计输出分数n有C[n]次。累计次数等于三时终止程序。(@线性搜索)
这三种方法在思维难度上各有差别,对空间和时间的要求,以及不同场景下的效率也不同。
程序简洁程度、编码难易程度、运算效率和内存使用都是选择算法的标准。
但运算效率和内存使用尤为重要。
伪代码 #
一种对算法的描述形式。
- 变量省略声明与类型
- 使用if while for 表示分支与跳转
- 不使用{} 只使用缩进
- operator遵循c/c++风格
- 数组的表达方式
- 长度 A.length
- 元素 A[i]
- 下标通常以0始(一些情况下可为1)
复杂度 #
复杂度用以评估算法的效率 。主要有以下两种规范:
- 时间复杂度
- 空间复杂度
通常我们所讨论的是时间复杂度。
**
大O表示法(The Big Oh Notation) #
**$O(g(n)) $**
我们以诸如$O(n^2)$的方式表达时间复杂度……其中n为问题的输入数据大小。
我们认为该算法复杂度与$g(n)$成正比 (并不严谨),亦称呼”为g(n)级的算法“。
对于引子的内容,若以更加一般的TOP N问题 表述——即对于m个整数,降序输出n个数,那么其对应的时间复杂度可分别表示为:
- $O(m * n)$
- $O(mlogm+n)$ 猜猜是哪种排序?
- $O(n+m+max(A[i]))$
根据g(n)的增长快慢,可以判断各个算法的优劣程度。
在实际动手之前,应该通过估算复杂度验证实用价值。
关于复杂度,更深入的内容:OI-wiki 复杂度
用以总结的入门例子 #
价差问题:
对$R_t$的一组数据,求得$R_j - R_i$的最大值($j>i$)

(艹 我第一反应想到的是$O(n^2)$的硬比)
# 其实是伪代码
# 复杂度为O(n)
minV = R[0]
maxV = -20000000 #初始得设小点 虽然我觉得可以跳过第一次循环的比较来解决
for j from 1 to n-1
maxV = max(maxV,R[j] - maxV)
minV = min(minV,R[j])
初等排序 #
插入排序的重点在于将数组分为已排序和未排序部分,且其对输入数据敏感。
对于冒泡排序,其逆序数能够反映一组数据的错乱程度。
选择排序的时间复杂度无论何时都为**$O(N^2)$**,它并不对输入敏感。
何谓排序?
数据按照键重新排列为升/降序的处理。
我们使用数组来管理数列形式的输入数据,然后通过循环处理完成元素的交换和移动,最终实现数据排序。
一般来说,我们的数据都是一张具有多种属性的表,所以排序时需要以特定元素作为基准,这个特定基准就被称为**“排序键”** 。
读者注:手动@STL的map类型……话说学过数据库的都知道键&表耶~
在挑选排序算法的时候,应当注意:
- 复杂度与稳定性
- 除保存数据的数组外是否需要其它内存
- 输入数据的特征是否会对复杂度造成影响
排序稳定性是指在一个序列中存在2个或以上键值相等的元素时,排序后 相对位置关系 不变。
插入排序 #
……它的思路与打扑克时排列手牌的方式类似……我们将牌一张张抽出来,分别插入到前面已排序好的手牌中的适当位置。重复这个操作直到插入最后一张牌即可。

#升序排列的插入排序
insSort(A, N)
for i from 0 to N - 1 # 我们对每一个未排序的元素展开相关操作
v = A[i] #当前的“未排序”元素
j = i - 1 #上一个元素
while j >=0 and a[j] > v #当 当前元素上一个元素存在,且上一个元素仍然大于当前元素时
A[j + 1] = A[j] #我们将上一个元素“后移”一位
j-- #移动到上上个元素
A[j + 1] = v #如果发现之前没有元素,或者它并不大于“未排序”元素 则把未排序元素怼到这个位置上
#include <stdio.h>
void trace(int a[], int sum)
{
for (int i = 0; i < sum; printf("%d ",a[i]), i++);
puts("");
}
void insSort(int a[], int sum)
{
for (int i = 0; i < sum;i++)
{
int v = a[i];
int j = 0;
for (j = i - 1; j >= 0 && a[j] >= v;a[j+1] = a[j], j--);
a[j + 1] = v;
}
}
int main()
{
int testArray[] = {2, 8, 6, 8, 4, 13, 89, 20, -30};
trace(testArray, sizeof(testArray) / sizeof(int));
insSort(testArray, sizeof(testArray) / sizeof(int));
puts("sorted:");
trace(testArray, sizeof(testArray) / sizeof(int));
return 0;
}
简短的总结:在插入排序中,我们主要依赖三个变量:
- 循环变量:即用于遍历整个数组的变量i
- 临时保存变量:即保存当前的“未排序”变量v
- 循环变量:即用于遍历整个已排序部分的变量j,用以寻找插入位置
考察
插入排序具有稳定性:元素只存在向后平移和插入,不相邻的元素不会直接交换位置。
复杂度:最坏情况下,考察得对于每个i循环都要执行i次,那么即$\sum_{i=1}^{n-1}i$ ,复杂度达到$O(N^2)$
注:估算时,在这里我们只关注多项式的最高次项——因为当N足够大时,其它项造成的影响可以忽略。
插入算法的复杂度受输入数据而大幅变化——因为当输入数据趋于有序,其时间复杂度将趋于$O(N)$。所以插入排序适合快速处理相对有序的数据。
冒泡排序 #
让数组像水中的气泡一样逐渐上浮……
读者注:我愿称之为两两相邻硬换法
(不给图了)
#升序排列
bubSort(A, N)
flag = true #旗帜为真
while flag #旗帜不倒
flag = false
for j from N -1 to 1 #倒序遍历整个数组
if A[j] < A[j - 1] #若当前数比前一个小
swap(A[j], A[j - 1]) #换到后面去
flag = true #旗帜为真
容易注意到,这个算法可以进行优化。因为每进行一次外层循环,将一定有一个较小元素被排到最前面。因此,每进行一次外层循环后,所需处理的未排序部分都会减少一个(看,冒泡泡!)。
因此我们可以修改:
for j from N -1 to 1
得到:
#升序排列
bubSort(A, N)
flag = true #旗帜为真
i = 0 #定义未排序部分下标
while flag #旗帜不倒
flag = false
for j from N -1 to i + 1 #倒序遍历整个数组
if A[j] < A[j - 1] #若当前数比前一个小
swap(A[j], A[j - 1]) #换到后面去
flag = true #旗帜为真
i++
#include <stdio.h>
void trace(int a[], int sum)
{
for (int i = 0; i < sum; printf("%d ",a[i]), i++);
puts("");
}
void bubSort(int a[], int sum)
{
for (int flag = 1, i = 0; flag; i++)
{
flag = 0;
for (int j = sum - 1; j > i; j--)
if(a[j] < a[j-1])
{
int temp = a[j];
a[j] = a[j - 1];
a[j - 1] = temp;
flag = 1;
}
}
}
int main()
{
int testArray[] = {2, 8, 6, 8, 4, 13, 89, 20, -30};
trace(testArray, sizeof(testArray) / sizeof(int));
bubSort(testArray, sizeof(testArray) / sizeof(int));
puts("sorted:");
trace(testArray, sizeof(testArray) / sizeof(int));
return 0;
}
简短的总结:在冒泡排序中,我们主要依赖两个变量:
- 循环变量:即变量i,表示未排序部分的终点
- 循环变量:即变量j,用以两两比较相邻元素
考察
冒泡排序具有稳定性:元素只存在相邻的元素交换位置。
若将比较部分的不等号添上等号,则会失去稳定性——相同的元素不一定保持原顺序
复杂度:最坏情况下,考察得对于每个循环的两两比较,那么即$\sum_{i=1}^{n-1}i$ ,复杂度达到$O(N^2)$
值得注意的是,“交换次数”更通用的名称是*“逆序数”**(亦作“反序数”),可以体现数列的错乱程度。*
选择排序 #
……一种直观的排序法,它会在每个计算步骤中选出一个最小值,进而完成排序。
读者注:就是不停地找一个区间的最小值,然后放到前面,继续缩小区间…… (参考之前实现TOP N的一种算法)
selSort(A, N)
for i from 0 to N - 1 #遍历整个数组
minJ = i #初始化当前区间内最小值
for j from i to N - 1 #遍历未排序区间
if A[j] < A[minJ] #确定该区间最小值下标
minJ = j
swap(A[i], A[minJ]) #把最小值dia过去
可以注意到,与冒泡排序一样,选择排序也在过程中将数组分割为已排序部分和未排序部分。
#include <stdio.h>
void trace(int a[], int sum)
{
for (int i = 0; i < sum; printf("%d ",a[i]), i++);
puts("");
}
void selSort(int a[], int sum)
{
for (int i = 0; i < sum; i++)
{
int minJ = i;
for (int j = i; j < sum; j++)
if(a[minJ]>a[j])
minJ = j;
int temp = a[i];
a[i] = a[minJ];
a[minJ] = temp;
}
}
int main()
{
int testArray[] = {2, 8, 6, 8, 4, 13, 89, 20, -30};
trace(testArray, sizeof(testArray) / sizeof(int));
selSort(testArray, sizeof(testArray) / sizeof(int));
puts("sorted:");
trace(testArray, sizeof(testArray) / sizeof(int));
return 0;
}
简短的总结:在选择排序中,我们主要依赖三个变量:
- 循环变量:即变量i,表示未排序部分的终点
- 临时变量:即变量minJ,用来存储未排序区间内最小元素的下标
- 循环变量:即变量j,用以遍历未排序部分
考察
选择排序具有不稳定性——它会直接交换两个不相邻的元素
在时间复杂度上,由于无论如何选择排序都进行N*N次循环,因此其复杂度永远为$O(N^2)$
——这也意味着它对输入数据不敏感。
*稳定排序 #
检测一个排序算法是否稳定。
对于一些特殊的表结构,我们关心其经过排序后是否仍然稳定。
这里简单介绍一种方法:即使用冒泡排序的结果与之一一比较即可。
希尔排序 #
暂时不学习
初等数据结构 #
数据结构是一种在程序中系统化管理数据集合的形式。
主要由以下三个概念组合而成:
- 数据集合:通过对象数据的本体保存数据集合。
- 规则:保证数据集合按照一定规矩进行正确操作、管理和保存的规则。
- 操作:对数据集合的操作,包括“插入”、“取出”、“查询数量”,“检索是否为空”等等。
对三种初等数据结构的简述 #
栈(Stack) #
……有效帮助我们临时保存数据……遵循LIFO(Last In First Out),先进后出原则。
基本操作
- push(x):添加元素x至栈顶
- pop():从栈顶取出元素
- isEmpty():检查栈是否为空
- isFull():检查栈是否已满
一般情况下,还包含“引用栈顶元素”和“检索指定数据”的操作。
规则
因为LIFO原则,pop出的元素总是最后一次push的元素。
队列(Queue) #
……是一个等待处理的行列……遵循FIFO(First In First Out),先进先出原则。
基本操作
- enqueue(x):在队列末尾添加元素x
- dequeue():从队列开头取出元素
- isEmpty():检查队列是否为空
- isFull():检查队列是否已满
一般情况下,还包含“引用对头元素”和“检索指定数据”的操作。
规则
因为FIFO原则,dequeue操作以元素被添加的先后顺序取出元素。
表(List) #
让数据保持一定顺序,又要对特定位置插入/删除。数组在此时或许值得一试,但其初始化即固定使用长度的模式在内存利用上十分不便。此时双向链表就能很好解决这一问题。并且,表型结构常常还在实现其它(高等)数据结构的过程中充当基础或零部件。
总结 #
程序中数据结构的种类和用法都能大幅影响算法效率。
栈 #
这里使用数组实现一个简单的栈。

init()
top = 0
isEmpty()
return top == 0
isFull()
return top >= MAX - 1
push(x)
assert(isFull())
top++
S[top] = x
pop()
assert(isEmpty())
top--
return S[top+1]
//array stack header
#ifndef A_STACK
#define A_STACK
#define aMAX 1000
#define aCap aMAX - 1
int aTop, aS[aMAX];
void a_init()
{
aTop = 0;
}
int a_is_empty()
{
return aTop == 0;
}
int a_is_full()
{
return aTop >= aCap;
}
void a_push(int x)
{
if(a_is_full())
return;
aTop++;
aS[aTop] = x;
}
int a_pop()
{
if(a_is_empty())
return 0;
aTop--;
return aS[aTop + 1];
}
#endif
-
S:存放栈数据
-
top:栈顶“‘指针“,它的值实时代表着元素数量
考察
下面这是一个可以解析逆波兰表达式进行四则运算的例子。
#include <stdio.h>
#include <stdlib.h>
#include "array_stack.h"
int main()
{
a_init();//初始化栈
int a = 0, b = 0;//初始化a,b变量,用以保存两个操作数
char buf[100];//输入缓存
int flag = 1;//循环控制变量
while(flag && scanf("%s", buf) != EOF)
{
//当读取到运算符时,取出栈中前两个元素进行运算,并将结果压回栈中
switch (buf[0])
{
case '+':
a = a_pop();
b = a_pop();
a_push(a + b);
break;
case '-':
a = a_pop();
b = a_pop();
a_push(b - a);
break;
case '*':
a = a_pop();
b = a_pop();
a_push(a * b);
break;
case '/':
a = a_pop();
b = a_pop();
a_push(b / a);
break;
//循环控制终止
case ',':
flag = 0;
break;
//如果读到的不是运算符,则必然是操作数,压入栈中
default:
a_push(atoi(buf));
break;
}
}
//得到栈顶最终结果
printf("calc: %d", a_pop());
return 0;
}
这个数组栈的pop与push复杂度均为$O(1)$
*一般情况下,数据结构多以结构体或类的形式实现。
队列 #
此处讲解如何使用数组实现一个存放整型数据的队列。

- Q:作为整型数组的队列
- head:队列头指针
- tail:队列尾指针
- enqueue(x):添加新元素至队尾
- dequeue():从队列头取出元素
然而,这样的队列存在天然的缺陷——
我们可以模拟一下队列进出的过程:

队列主体部分不断地向着数组末尾移动……
很自然地,我们想到在每次dequeue操作后,将数据整体向左移动,然而$O(N)$的复杂度确实令人望而生畏(链表赛高)……
为了解决这个问题,我们可以将这个一维数组视为一段环形缓冲区来管理。

……指示队列范围的head和tail指针在超出数组范围hi重新从数组开头进行循环……
为了区分队列的空与满,我们可以规定tail至head中至少有一个空位(tail指向空位)
奇妙伪代码:
init()
head = tail = 0 #初始化 头尾指针位置 为0(一维数组起始)
isEmpty()
return head == tail #我们认为头尾相等就是空
isFull()
head == (tail + 1) % MAX #我们认为头尾差一格就是满 用这个表达式巧妙地体现了这个关系
enqueue(x)
assert(isFull()) #检查非法操作
Q[tail] = x
tail = (tail + 1 == MAX) ? 0 : tail + 1 #将越界情况下的结果约束在数组范围
dequeue()
assert(isEmpty()) #检查非法操作
x = Q[head]
head = (head + 1 == MAX) ? 0 : head + 1 #将越界情况下的结果约束在数组范围
return x
//circular queue header
//为了通用性,将存储类型改为void*
#ifndef C_QUEUE
#define C_QUEUE
#define cMAX 100
int cHead, cTail;
void* cQ[cMAX];
void c_init()
{
cHead = cTail = 0;
}
int c_is_empty()
{
return cHead == cTail;
}
int c_is_full()
{
return cHead == (cTail + 1) % cMAX;
}
void c_enqueue(void* x)
{
if(c_is_full())
return;
cQ[cTail] = x;
cTail = (cTail + 1) % cMAX;
}
void* c_dequeue()
{
if(c_is_empty())
return NULL;
void* x = cQ[cHead];
cHead = (cHead + 1) % cMAX;
return x;
}
#endif
考察
用数组实现队列时,关键在于如何有效利用内存,以及如何将enqueue和dequeue的算法复杂度控制在$O(1)$。
只要使用环形缓冲区就同时能做到哦!
示例应用
读者注:作为学软工的,原文的竞赛风格代码实在不是很合适,遂有小小地修改。
现有名称为$name$且处理时间为$time_i$的$n$个任务排成一列,CPU通过循环调度法逐一处理这些任务,每个任务最多处理$q$ms(即时间片)。如果$q$ms之后任务尚未处理完毕,那么该任务将被移动至队伍最末尾,CPU随即开始处理下一个任务。
现在:
输入
- 输入形式如下:
- $count$ $max time$
- $name_1$ $time_1$
- $name_2$ $time_2$
- $name_3$ $time_3$
- ……
- $name_n$ $time_n$
输出
- 每执行一个时间片的任务一次,输出当前任务执行所用时间、剩余时间、自调度开始所经时间。
- 当任务结束时,输出该任务结束信息,附自调度开始所经时间。
限制
$1\le n \le 100 000$
$1\le q \le 1000$
$1\le time_i \le 50 000$
$1\le name_i.length \le 100 000$
$1\le \sum_{}^{}name_i \le 100 000$
随便你,不就是count,time,name长之类的玩意吗……能跑就行
输入示例
5 100 pvz 150 mc 80 nekopara 200 sg 350 ys 20
输出示例
starting the simulation.pvz has run 100 ms, with 50 ms left. mc has run 80 ms, with 0 ms left. mc has ended. it’s 180 ms now. nekopara has run 100 ms, with 100 ms left. sg has run 100 ms, with 250 ms left. ys has run 20 ms, with 0 ms left. ys has ended. it’s 400 ms now. pvz has run 50 ms, with 0 ms left. pvz has ended. it’s 450 ms now. nekopara has run 100 ms, with 0 ms left. nekopara has ended. it’s 550 ms now. sg has run 100 ms, with 150 ms left. sg has run 100 ms, with 50 ms left. sg has run 50 ms, with 0 ms left. sg has ended. it’s 800 ms now.
#include <stdio.h>
#include <stdlib.h>
#include <Windows.h>
#include "circular_queue.h"
#define MIN(a,b) (((a) < (b)) ? (a) : (b))
int elaps = 0, count = 0, maxTime = 50, delta = 0;//时长,任务数,时间片长度,时间差值
//任务结构体定义
typedef struct myProcess
{
char name[50];
int timeLapse;
}P;
//跑任务的函数
void run_process()
{
P *p = (P*)c_dequeue();//取出队列内容
if(p != NULL)//有效值
{
delta = MIN(maxTime, p->timeLapse);//计算差值:考虑当前时间片是否满足剩余时长
Sleep(p->timeLapse); //模拟玩的,可以不写
p->timeLapse -= delta;//减去任务时间
elaps += delta;//累加总时长
printf("%s has run %d ms, with %d ms left.\n", p->name, delta, p->timeLapse);//输出信息
if(p->timeLapse)//如果还有时长,重新加入队列等待执行
c_enqueue(p);
else
{
printf("%s has ended. it's %d ms now.\n", p->name, elaps);//结束信息
free(p);//释放内存
}
}
}
int main()
{
c_init();//初始化队列
puts("please set task arguments.");
scanf("%d %d", &count, &maxTime);//读入几个参数
for (int i = 0; i < count; i++)
{
P *t = (P*)malloc(sizeof(P));//开辟内存,创建进程/任务
scanf("%s %d", t->name, &t->timeLapse);//读入任务信息
c_enqueue((void *)t);//添加进入队列
}
//利用一行for完成提示信息输出+调度循环
for (puts("starting the simulation.");(!c_is_empty());run_process());
return 0;
}
链表 #
某些技巧需要满足数据的动态变化。在实现它们的时候,编程者需要具备适时申请或释放内存的技巧。
双向列表的基本结构
略有修改,增加安全性和通用性

如图所示,表中的个元素称为“结点”。双向链表的结点是结构体,由数据本体、指向前一元素的指针prev以及指向后一元素的指针next组成。这些结构体通过指针连接成一个链,就形成了双向链表。
typedef struct dNode{
int key;
dNode *prev;
dNode *next;
}dNode;
……在表头设置一个特殊结点可以简化链表的实现……即头结点。它虽然不包含实际数据,但可以帮助我们更轻松地对链表做出更改。
dNode* d_list_init()//初始化:生成一个头结点
{
dNode *nil = (dNode *)malloc(sizeof(dNode));
//头结点前后指针初始化均指向自身
nil->prev = nil;
nil->next = nil;
return nil;
}
我们现在添加一个插入元素的过程:

void d_list_ins(dNode *head, int key)//在头结点后插入一个结点
{
if (head == NULL)
return;
dNode *n = (dNode *)malloc(sizeof(dNode));
n->key = key;
n->next = head->next;
head->next->prev = n;
head->next = n;
n->prev = head;
}
现在我们加入线性搜索指定结点的过程:
dNode* d_list_search(dNode *head, int key)
{
if (head == NULL)
return head;
dNode *cur;
//从头结点的下一节点开始直到末尾遍历
//cur != head:当刚好回到头结点(链表为空;或走完链表,因为尾结点的next就是头结点)时结束
for (cur = head->next; cur != head && cur->key != key; cur = cur->next);
return cur;
}
删除指定结点:

void d_list_delete(dNode *head, dNode *n)
{
if (n == NULL || n == head)
return;
n->prev->next = n->next;
n->next->prev = n->prev;
free(n);
}
写了一些宏
#define DLIST_DEL_FIRST(head) d_list_delete(head, head->next)
#define DLIST_DEL_LAST(head) d_list_delete(head, head->prev)
#define DLIST_DEL_AT(head, key) d_list_delete(head, d_list_search(head, key))
考察
双向链表算法复杂度为$O(1)$。
搜索的复杂度为$O(N)$。
一般的删除操作复杂度为$O(1)$,但涉及到指定key的删除,则为$O(N)$。
此处介绍的双向链表搜索和删除的复杂度均为$O(N)$,对于单个链表的实现而言,应用价值不大。但它将作为其它数据结构的基础/零部件发挥作用。
示例应用(简化版)
实现一个程序,支持以下几种命令输入:
- ins x
- del x
- del F
- del L
- srch x
- end
示例输入&输出:
pls enter your instructions: ins 20 ins 30 ins 40 ins 180 ins 360 srch 30 founded. srch 181 not founded. del F deleted. del L deleted. del 180 deleted. end key remains: 40 key remains: 30
示例代码:
//double linked list header
#ifndef D_LIST
#define D_LIST
#include <malloc.h>
typedef struct dNode{
int key;
struct dNode *prev;
struct dNode *next;
}dNode;
dNode* d_list_init()
{
dNode *nil = (dNode *)malloc(sizeof(dNode));
nil->prev = nil;
nil->next = nil;
return nil;
}
void d_list_ins(dNode *head, int key)
{
if (head == NULL)
return;
dNode *n = (dNode *)malloc(sizeof(dNode));
n->key = key;
n->next = head->next;
head->next->prev = n;
head->next = n;
n->prev = head;
}
dNode* d_list_search(dNode *head, int key)
{
if (head == NULL)
return head;
dNode *cur;
for (cur = head->next; cur != head && cur->key != key; cur = cur->next);
return cur;
}
void d_list_delete(dNode *head, dNode *n)
{
if (n == NULL || n == head)
return;
n->prev->next = n->next;
n->next->prev = n->prev;
free(n);
}
#define DLIST_DEL_FIRST(head) d_list_delete(head, head->next)
#define DLIST_DEL_LAST(head) d_list_delete(head, head->prev)
#define DLIST_DEL_AT(head, key) d_list_delete(head, d_list_search(head, key))
#endif
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include "d_list.h"
int main()
{
dNode *head = d_list_init();
char input[100];
int flag = 0;
//初始化提示语句,获取正确输入,若输入为end就终止循环
for (puts("pls enter your instructions:"); scanf("%s", input) && strcmp(input,"end");)
{
//判断命令类型
if(!strcmp(input, "ins"))
flag = 1;
else if(!strcmp(input, "del"))
flag = 2;
else if(!strcmp(input, "srch"))
flag = 3;
else{
flag = 0;
puts("wrong input.");
continue;
}
//获取第二个命令
scanf("%s", input);
//分类讨论
switch (flag)
{
case 1:
d_list_ins(head, atoi(input));
break;
case 2:
switch (input[0])
{
case 'F':
DLIST_DEL_FIRST(head);
break;
case 'L':
DLIST_DEL_LAST(head);
break;
default:
DLIST_DEL_AT(head, atoi(input));
break;
}
puts("deleted.");
break;
case 3:
if (d_list_search(head, atoi(input)) != head)
puts("founded.");
else
puts("not founded.");
break;
}
}
//打印全部内容
for (dNode *cur = head->next; cur != head; printf("key remains: %d\n",cur->key), cur=cur->next);
return 0;
}
不要学我这种写for循环的习惯
C++ STL(标准库)——一些容器 #
std::stack<T> #
对栈元素的操作复杂度均为$O(1)$
| top() | 返回一个栈顶元素的引用,类型为 T&。如果栈为空,返回值未定义 |
| push(const T& obj) | 可以将对象副本压入栈顶。这是通过调用底层容器的 push_back() 函数完成的 |
| push(T&& obj) | 以移动对象的方式将对象压入栈顶。这是通过调用底层容器的有右值引用参数的 push_back() 函数完成的 |
| pop() | 弹出栈顶元素 |
| size() | 返回栈中元素的个数。 |
| empty() | 在栈中没有元素的情况下返回 true |
| emplace() | 用传入的参数调用构造函数,在栈顶生成对象 |
| swap(stack |
将当前栈中的元素和参数中的元素交换。参数所包含元素的类型必须和当前栈的相同。对于 stack 对象有一个特例化的全局函数 swap() 可以使用 |
std::queue<T> #
对队列成员的操作复杂度均为$O(1)$
| front() | 返回 queue 中第一个元素的引用。如果 queue 是常量,就返回一个常引用;如果 queue 为空,返回值是未定义的 |
| back() | 返回 queue 中最后一个元素的引用。如果 queue 是常量,就返回一个常引用;如果 queue 为空,返回值是未定义的 |
| push(const T& obj) | 在 queue 的尾部添加一个元素的副本。这是通过调用底层容器的成员函数 push_back() 来完成的 |
| push(T&& obj) | 以移动的方式在 queue 的尾部添加元素。这是通过调用底层容器的具有右值引用参数的成员函数 push_back() 来完成的 |
| pop() | 删除 queue 中的第一个元素 |
| size() | 返回 queue 中元素的个数 |
| empty() | 如果 queue 中没有元素的话,返回 true |
| emplace() | 用传给 emplace() 的参数调用 T 的构造函数,在 queue 的尾部生成对象 |
| swap(queue |
将当前 queue 中的元素和参数 queue 中的元素交换。它们需要包含相同类型的元素。也可以调用全局函数模板 swap() 来完成同样的操作 |
std::vector<T> #
这是变长数组
其中,插入、删除操作的复杂度为$O(N)$,其它操作均为$O(1)$。
部分成员函数:
| size() | 返回元素数。 |
| push_back(x) | 在vector末尾添加元素x |
| begin() | 指向开头的迭代器 |
| end() | 指向末尾的迭代器 |
| insert(p, x) | 在p的位置插入x |
| erase(p) | 删除位置为p的元素 |
| clear()删除所有元素 | 删除所有元素 |
std::list<T> #
这是双向链表
对元素的操作复杂度大都为$O(1)$。
| void push_front(const T & val) | 将 val 插入链表最前面 |
| void pop_front() | 删除链表最前面的元素 |
| void sort() | 将链表从小到大排序 |
| void remove (const T & val) | 删除和 val 相等的元素 |
| remove_if | 删除符合某种条件的元素 |
| void unique() | 删除所有和前一个元素相等的元素 |
| void merge(list |
将链表 x 合并进来并清空 x。要求链表自身和 x 都是有序的 |
| void splice(iterator i, list |
在位置 i 前面插入链表 x 中的区间 [first, last),并在链表 x 中删除该区间。链表自身和链表 x 可以是同一个链表,只要 i 不在 [first, last) 中即可 |
应用题 #
wow 是洋文的欸
Areas on the Cross-Section Diagram #
Your task is to simulate a flood damage.
For a given cross-section diagram, reports areas of flooded sections.
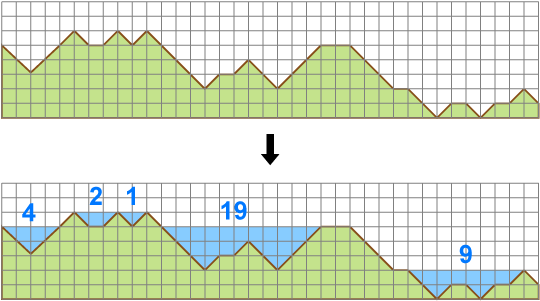
Assume that rain is falling endlessly in the region and the water overflowing from the region is falling in the sea at the both sides. For example, for the above cross-section diagram, the rain will create floods which have areas of 4, 2, 1, 19 and 9 respectively.
Input #
A string, which represents slopes and flatlands by ‘/’, ‘' and ‘’ respectively, is given in a line. For example, the region of the above example is given by a string “\///_//\\//\///__\_\///".
output #
Report the areas of floods in the following format:
$A$ $k$ $L_1$ $L_2$ … $L_k$
In the first line, print the total area $A$ of created floods.
In the second line, print the number of floods $k$ and areas $L_i (i = 1, 2, ..., k)$ for each flood from the left side of the cross-section diagram. Print a space character before $L_i$.
Constraints #
- $1 \leq$ length of the string $\leq 20,000$
Sample Input 1 #
\\//
Sample Output 1 #
4
1 4
Sample Input 2 #
\\///\_/\/\\\\/_/\\///__\\\_\\/_\/_/\
Sample Output 2 #
35
5 4 2 1 19 9
Answer by the reader #
我真傻 真的 我单知道逆波兰表达式可以用栈 我不知道栈还可以……
#include <cstdio>
#include <cstdlib>
#include <vector>
#include <stack>
//定义一个存放水域的结构体
struct w_area
{
int start_pos;//左起始点‘\’位置
int area;//水域面积
};
int main()
{
std::stack<int> inputs;//存放输入‘\’
std::stack<w_area> areas;//存放所有水域
int total = 0, i = 0;//总面积,计数(当前位置)变量
for (char ch = '_', flag = 0; scanf("%c", &ch) && ch!='\n'; i++)//读入输入,并计数
{
switch (ch)
{
case '\\':
inputs.push(i);//向栈中压入一个‘\’
break;
case '/':{
if (!inputs.empty())//如果输入栈不为空:即当前右侧的‘/’
{
int j = inputs.top();//获取最近一个‘\’的位置,其必然与当前‘/’配对
inputs.pop();//弹出栈
int a = i - j;//前后距离即为当前一组水域的面积
total += a;//加入总面积
w_area latest = {j, a};//记录当前的水域
//如果之前已经记录了水域
//且之前那组水域的起始位置更大,意味着它在新水域——即事实上更前面的一组水域之后(之下)
//我们更新当前水域,它将合并上一组水域(它之后水域)的面积
//同时弹出已经被合并掉的旧水域
//一直循环至无法合并为止
for (; (!areas.empty()) && (areas.top().start_pos > j);
latest.area+=areas.top().area, areas.pop());
//将当前水域压入栈中
areas.push(latest);
}
break;
}
case '_':
break;
default:
puts("wrong input.");
break;
}
}
//注意:_Get_container()方法在一些环境下可能不受支持,此时考虑其他方法逆序输出即可
auto area_content = areas._Get_container();
printf("%d\n%d", total, area_content.size());
for (auto it = area_content.begin(); it != area_content.end(); printf(" %d", it->area), it++);
return 0;
}
搜索 #
所谓搜索,就是在数据集合中寻找给定关键字的位置或判断其有无……
- 线性搜索
- 二分搜索
- 散列法
