变换和观察
#

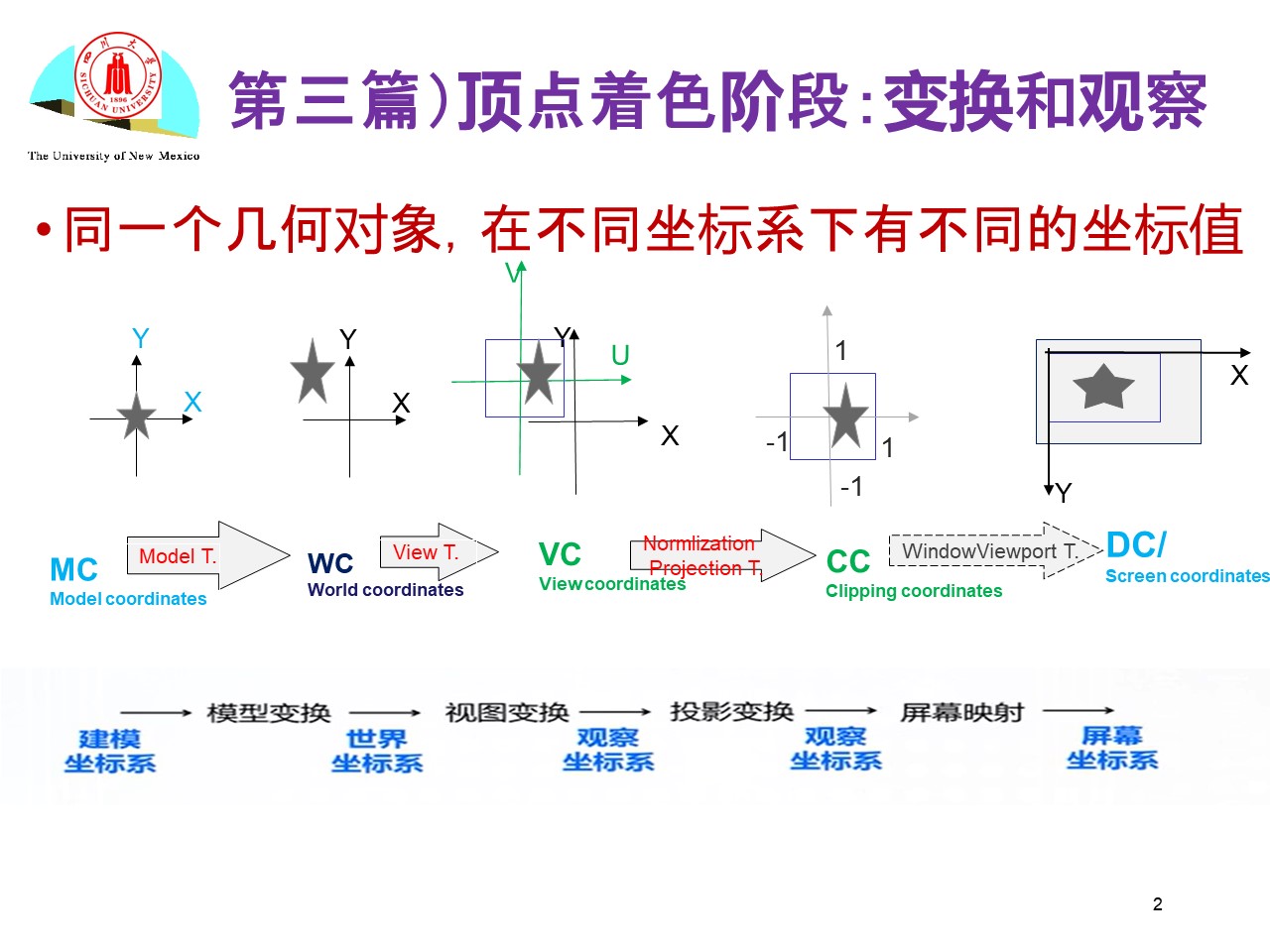
坐标体系
#

针对一组基向量，线性表出空间中的一个位置元素，例如： $v=2v_1+3v_2-4v_3$

即

$v=[2,3,-4]^T$（通常使用列向量的表示）

变换坐标系：对于一对基向量：

$[u_1,u_2,u_3]=M^T[v_1,v_2,v_3]$

则在v坐标系下的向量$α$在u下是$β=M^Tα$

在仿射空间中，通过基向量+原点形成~

何为齐次坐标？

齐次坐标：给普通的向量空间增加一个元素，用于区分表达向量表示的是一个方向还是一点

四维齐次坐标：

$v=[α_1,α_2,α_3,0],p=[β_1,β_2,β_3,1]$

优点：使得所有基本变换可以通过变换矩阵描述

思想：把n维集合问题变换到n+1维

形式上：用n+1维向量表示n维向量

$笛卡尔坐标(x,y)→齐次坐标(xh,yh,h),(h≠0,规格化齐次坐标下h=1)$

Frame的变换

假设两个frame：$P(P_0,v_1,v_2,v_3), Q(Q_0,u_1,u_2,u_3)$

对应一个4x4变换矩阵$M$：

$$ \left( \begin{matrix} γ_{11}&γ_{12}&γ_{13}&0\\ γ_{21}&γ_{22}&γ_{23}&0\\ γ_{31}&γ_{32}&γ_{33}&0\\ γ_{41}&γ_{42}&γ_{43}&1\\ \end{matrix} \right) $$

（自由度只有12个）

何为变换：

映射点/向量到别的点/向量

旋转（刚性）
- $$ R_z(θ)=\left( \begin{matrix} cosθ&-sinθ&0&0\\ sinθ&cosθ&0&0\\ 0&0&1&0\\ 0&0&0&1\\ \end{matrix} \right) $$
- $$ R_x(θ)=\left( \begin{matrix} 1&0&0&0\\ 0&cosθ&-sinθ&0\\ 0&sinθ&cosθ&0\\ 0&0&0&1\\ \end{matrix} \right) $$
- $$ R_y(θ)=\left( \begin{matrix} cosθ&0&sinθ&0\\ 0&1&0&0\\ -sinθ&0&cosθ&0\\ 0&0&0&1\\ \end{matrix} \right) $$
- $$
平移（刚性）
- $P'=P+d$
- 齐次坐标：$P=TP$
- $$ T=\left( \begin{matrix} 1&0&0&d_x\\ 0&1&0&d_y\\ 0&0&1&d_z\\ 0&0&0&1\\ \end{matrix} \right) $$
缩放
- $$ S=\left( \begin{matrix} s_x&0&0&0\\ 0&s_y&0&0\\ 0&0&s_z&0\\ 0&0&0&1\\ \end{matrix} \right) $$
镜像
- 缩放符号变号
斜切
- $略$